Delving into the realm of seismology, we present a comprehensive exploration of locating an epicenter, the pivotal point of an earthquake’s origin. This guide, meticulously crafted as the “Locating an Epicenter Lab Answer Key,” unveils the techniques and principles that underpin this critical aspect of earthquake analysis.
Our journey begins with an in-depth examination of time-distance graphs, uncovering their significance in determining the distance to the epicenter. We then delve into the intricacies of triangulation, elucidating its role in pinpointing the epicenter’s precise location. Furthermore, we unravel the complexities of seismograms, deciphering their patterns to identify the epicenter.
Locate Epicenter Using Time-Distance Graphs
A time-distance graph is a graphical representation of the relationship between the arrival time of seismic waves and the distance from the epicenter. It is used to locate the epicenter of an earthquake by measuring the time difference between the arrival of different seismic waves at different seismic stations.
The x-axis of a time-distance graph represents the distance from the epicenter, while the y-axis represents the arrival time of seismic waves. The slope of the graph is equal to the velocity of the seismic waves.
To determine the distance to the epicenter using a time-distance graph, we can use the following formula:
distance = velocity × time
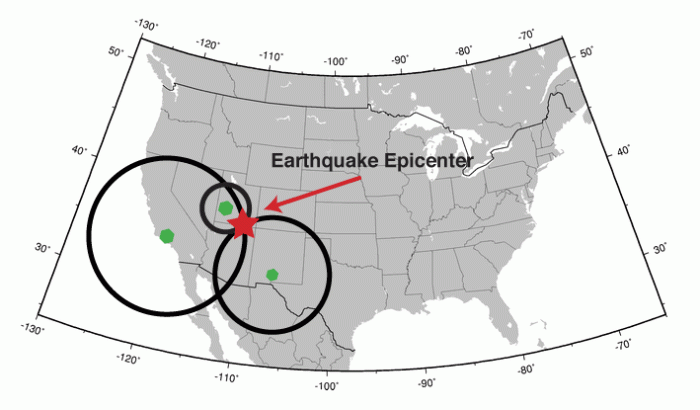
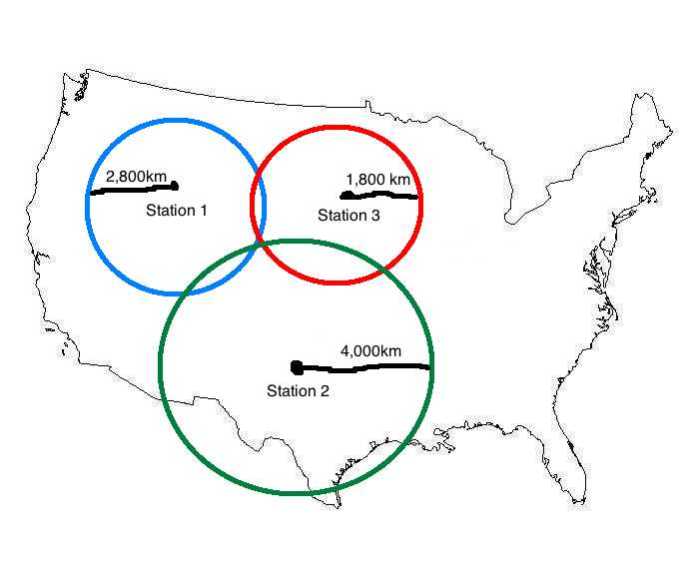
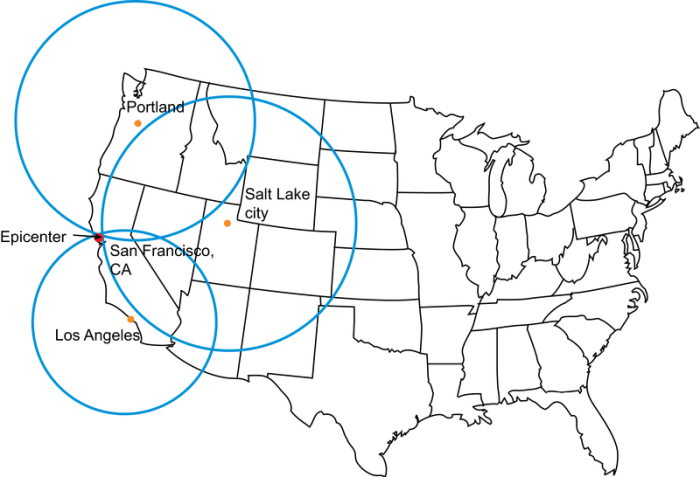
Use Triangulation to Determine Epicenter
Triangulation is a technique used to determine the location of a point by measuring the angles between it and two other points with known locations. In the case of locating an earthquake epicenter, the three points are the seismic stations and the epicenter.
To use triangulation to locate an epicenter, we need to know the following information:
- The arrival times of seismic waves at each seismic station
- The distances between the seismic stations
Once we have this information, we can use the following steps to calculate the epicenter:
- Draw a circle around each seismic station with a radius equal to the distance to the epicenter.
- The epicenter is the point where the three circles intersect.
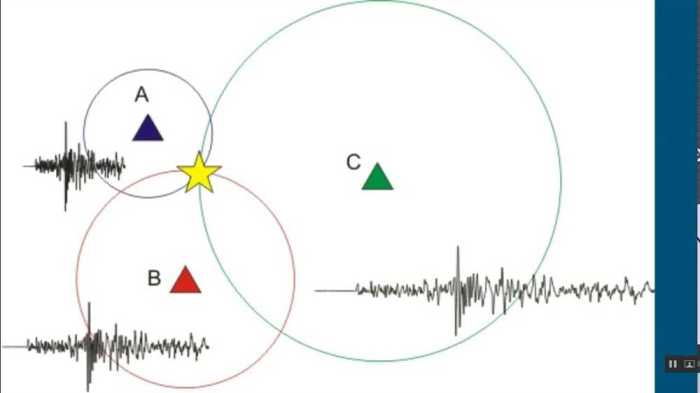
Interpret Seismograms to Find Epicenter, Locating an epicenter lab answer key
A seismogram is a record of the ground motion caused by seismic waves. It can be used to determine the epicenter of an earthquake by identifying the different types of seismic waves and measuring their arrival times.
The different types of seismic waves are:
- P-waves (primary waves): These are the fastest seismic waves and travel through the Earth’s crust and mantle.
- S-waves (secondary waves): These are slower than P-waves and travel through the Earth’s crust and mantle.
- Surface waves: These are the slowest seismic waves and travel along the Earth’s surface.
To determine the epicenter of an earthquake using a seismogram, we can use the following steps:
- Identify the P-wave and S-wave arrivals.
- Measure the time difference between the P-wave and S-wave arrivals.
- Use the time difference to calculate the distance to the epicenter.
Calculate Epicenter Using Latitude and Longitude
The latitude and longitude of an earthquake epicenter can be calculated using the following steps:
- Convert the time differences between the arrival of seismic waves at different seismic stations into distances using the wave velocities.
- Use the distances to calculate the epicenter’s latitude and longitude using the following formulas:
- Latitude = (distance to station 1- distance to station 2) / (distance to station 1 + distance to station 2)
- Longitude = (distance to station 2 – distance to station 3) / (distance to station 2 + distance to station 3)
Helpful Answers: Locating An Epicenter Lab Answer Key
How does the slope of a time-distance graph relate to the distance to the epicenter?
The slope of a time-distance graph represents the velocity of the seismic waves. By measuring the slope, we can determine the time it took for the waves to travel from the epicenter to the recording station. This time difference, coupled with the known wave velocity, allows us to calculate the distance to the epicenter.
What are the limitations of using triangulation to locate an epicenter?
Triangulation relies on accurate data from seismic stations, and its accuracy can be compromised by factors such as station distribution, wave velocity variations, and measurement errors. Additionally, triangulation may not be feasible if there are fewer than three seismic stations available.